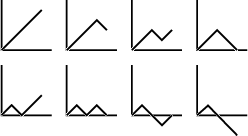
Oplossingen week 8 (21 t/m 27 februari)

Zig-zag-paden

Maandag 21 februari:

Ziehier de 8 mogelijke paden die beginnen met een stap vooruit. De paden die beginnen met een stap achteruit krijg je door deze 8 te spiegelen in de x-as. In 4 seconden kunnen alle punten (4,y) met y = -4, -2, 0, 2, 4 worden bereikt.

Dinsdag 22 februari:

Na t seconden kan ieder punt van de vorm (t, -t+2k) met 0kt worden bereikt.

Woensdag 23 februari:

Als je na 10 stappen in het punt (10,6) bent, heb je 8 stappen vooruit en 2 stappen achteruit gemaakt. Het gevraagde aantal is dus gelijk aan het aantal tijdstippen waarop de twee stappen achteruit zijn gemaakt. Als de eerste stap achteruit in seconde t is gemaakt, zijn er voor de tweede nog 10-t mogelijkheden. Het aantal is dus 9+8+...+2+1=45.

Donderdag 24 februari:

Stel P positieve en N negatieve stappen. Dan is P+N=119, P-N=87. Dus (optellen) 2P=206, P=103, N=16.

Vrijdag 25 februari:

Op dezelfde manier als in het probleem van donderdag vind je dat er (n+k)/2 positieve en (n-k)/2 negatieve stappen zijn gemaakt. Het gevraagde aantal is dus alvast 0 als n+k oneven is. Als n+k even is, is het aantal gelijk aan de binomiaalcoëfficient n boven (n-k)/2: n! / ((n+k)/2)!((n-k)/2)!.

Zaterdag 26 februari:

Stel P is een pad van A naar B dat de x-as ergens raakt of kruist. Dan is er ook een eerste ("vroegste") punt x₀ waar P de x-as raakt of kruist. Als je nu het deel van P tussen x_A en x₀ spiegelt t.o.v. de x-as, dan heb je een pad van A' naar B. Omgekeerd kun je vanuit ieder pad van A' naar B op die manier een pad van A naar B maken dat de x-as ergens raakt of kruist.

Zondag 27 februari:

Neem aan dat m>0, k>0 en dat n+k-m even is. Het totale aantal paden van (0,n) naar (n,k) is dan n boven (n+k-m)/2 (= P₁). Volgens de truc van zaterdag zijn er n boven (n+k+m)/2 (= P₂) paden van (0,m) naar (n,k) die de x-as ergens raken of kruisen. Het gevraagde aantal is dus P₁-P₂.